MathJax

To be applicable, the Lennard-Jones potential function is converted first into coordinates instead of radius distances so that exact positions can extrapolated instead of arbitrary distances which may not be feasible in certain circumstances or require higher dimensions. The function is changed using the Euclidean distance in place of the radius.
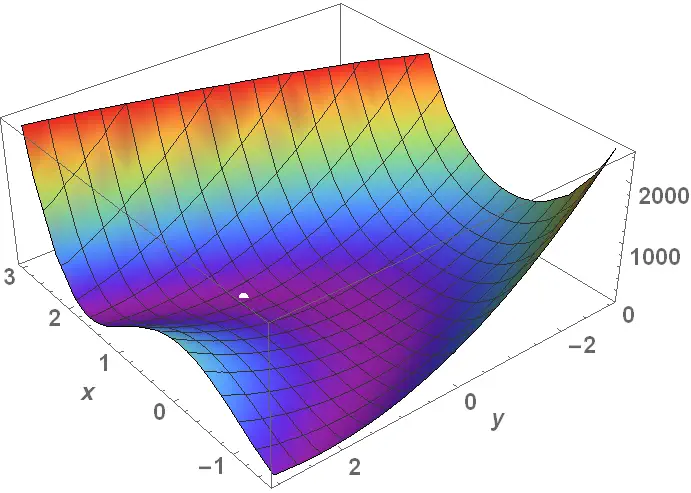
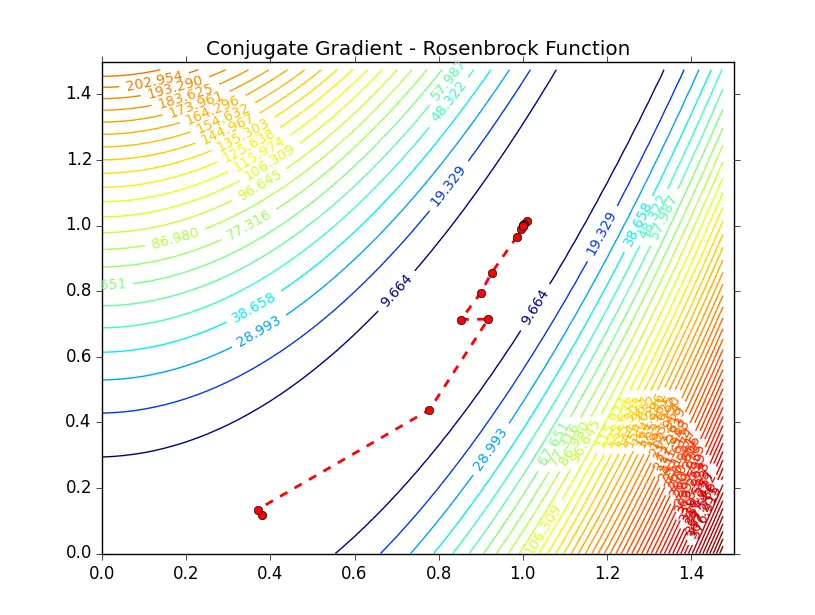
$$ V_{LJ} = \sum_{i} \left[ \frac{4}{\sqrt{(x_i-x_j)^2+(y_i-y_j)^2+(z_i-z_j)^2}^{12}} - \frac{4}{\sqrt{(x_i-x_j)^2+(y_i-y_j)^2+(z_i-z_j)^2}^{6}} \right] $$Then the process becomes solving for each \(x\), \(y\), and \(z\) coordinate for the atoms. When looking at 2 atoms the objective function has 6 variables and is already more complex than solving the simple 2 dimensional minimum of the Rosenbrock function.
$$ \text{min}~V_{LJ}=\left[ \frac{4}{\sqrt{(x_1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2}^{12}} - \frac{4}{\sqrt{(x_1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2}^{6}} \right] $$Some of this complexity can be avoided by setting one atom at the origin to be the reference for the coordinates of the remaining atoms.